Kategoria: Bez kategorii

Bazowa architektura. Koncepcja.

Feature space

Separating hyperplane

W jaki sposób zwizualizować predykcje sztucznych sieci neuronowych?

Skrót:
Mając możliwość zakładu o pieniądze np. zyskanie lub stracenie 10zł na tym, że coś się stanie, możemy to policzyć w ten sposób

E = P(X=x)

Przykładowo: Szansa na to, że ktoś słyszał o danym filmie wynosi 20%, oraz 80%, że nie słyszał.

Jeżeli ktoś słyszał to zyskujemy 10zł, jeżeli nie to tracimy 10zł

Równanie: -10*0.2 + 10*0.8 = -2 + 8 = 6, średnio zyskujemy 6zł na każdym zakładzie

Entropia

Entropia może być wykorzystana do tworzenia Drzew klasyfikujących

Może również posłużyć do określania mutual information (informacji wzajemnej) https://pl.wikipedia.org/wiki/Informacja_wzajemna

Pomagając określić związek między dwoma rzeczami.

Softmax korzysta z funkcji e f(x) = e^x to obliczania prawdopodobieństwa (binarnego), ponieważ funkcja ta nie posiada ujemnych wartości, nawet dla negatywnych argumentów

Softmax to o suma to 1

tbd
W skrócie A(M,N) * B(N,K) = C(M,K)

Dla wektorów 1D \( \mathbf{a} \) i \( \mathbf{b} \):
\[
\mathbf{a} = [a_1], \quad \mathbf{b} = [b_1]
\]
Iloczyn skalarny:
\[
\mathbf{a} \cdot \mathbf{b} = a_1 \cdot b_1
\]

Dla wektorów 2D \( \mathbf{a} \) i \( \mathbf{b} \):
\[
\mathbf{a} = [a_1, a_2], \quad \mathbf{b} = [b_1, b_2]
\]
Iloczyn skalarny:
\[
\mathbf{a} \cdot \mathbf{b} = a_1 \cdot b_1 + a_2 \cdot b_2
\]

Dla macierzy 3×3 \( \mathbf{A} \) i \( \mathbf{B} \):
\[
\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix}
\]

Możemy obliczyć iloczyn skalarny między odpowiadającymi sobie wierszami \( \mathbf{A} \) i kolumnami \( \mathbf{B} \).

Przyjmując wiersz \( i \) z macierzy \( \mathbf{A} \) i kolumnę \( j \) z macierzy \( \mathbf{B} \):
\[
\mathbf{A}_i \cdot \mathbf{B}^j = a_{i1} \cdot b_{1j} + a_{i2} \cdot b_{2j} + a_{i3} \cdot b_{3j}
\]

Na przykład, dla wiersza 1 i kolumny 1:
\[
\mathbf{A}_1 \cdot \mathbf{B}^1 = a_{11} \cdot b_{11} + a_{12} \cdot b_{21} + a_{13} \cdot b_{31}
\]

Wynikiem jest skalar, pojedyncza liczba, bez wzlgędu na to jak duża jest macierz.
Dot product – Iloczyn skalarny możliwy jest tylko dla macierzy lub vectorów O TYM SAMYM ROZMIARZE.
Jest to numer wskazujący na podobieństwa między dwoma obiektami, wektorami, macierzami, tensorami, sygnałami, zdjęciami.

Przykład w pyTorch:
tv1 = torch.tensor([1,2,4,-2]
tv2 = torch.tensor([3,4,1,3]
print(torch.dot(tv1, tv2)) # via function
print(torch.sum(tv1*tv2)) # Via computation
The result is a tensor!

A column vector:
\[
\mathbf{v} =
\begin{bmatrix}
v_1 \\
v_2 \\
v_3
\end{bmatrix}
\]

Transposed to a row vector:
\[
\mathbf{v}^T =
\begin{bmatrix}
v_1 & v_2 & v_3
\end{bmatrix}
\]

Which is equivalent to:
\[
\mathbf{\begin{bmatrix}
v_1 \\
v_2 \\
v_3
\end{bmatrix}}^T =
\begin{bmatrix}
v_1 & v_2 & v_3
\end{bmatrix}
\]
And:
\[
\mathbf{\begin{bmatrix}
v_1 & v_2 & v_3
\end{bmatrix}}^T =
\begin{bmatrix}
v_1 \\
v_2 \\
v_3
\end{bmatrix}
\]

And for a double/multiple column vector transposed to a row vector:

\[
\mathbf{\begin{bmatrix}
v_1 & v_4 \\
v_2 & v_5 \\
v_3 & v_6
\end{bmatrix}}^T =
\begin{bmatrix}
v_1 & v_2 & v_3 \\
v_4 & v_5 & v_6
\end{bmatrix}^T =
\begin{bmatrix}
v_1 & v_4 \\
v_2 & v_5 \\
v_3 & v_6
\end{bmatrix}
\]

ANN – Artificial neural network (Student behavior -> exam outcome)

CNN – Convolutional neural network (Classify picture -> cat?)

RNN – Recurrent neural network (Audio clip of cough -> has covid?)

Linear Functions

import torch.nn as nn
input_tensor = torch.tensor([[0.3471, 0.4547, -0.2356]])

Pass it to linear layer to apply a linear function

linear_layer = nn.Linear(in_features=3,out_features=2)

output = linear_layer(input_tensor)

Each layer has a .weight and .bias propert

linear_layer.weight & linear_layer.bias

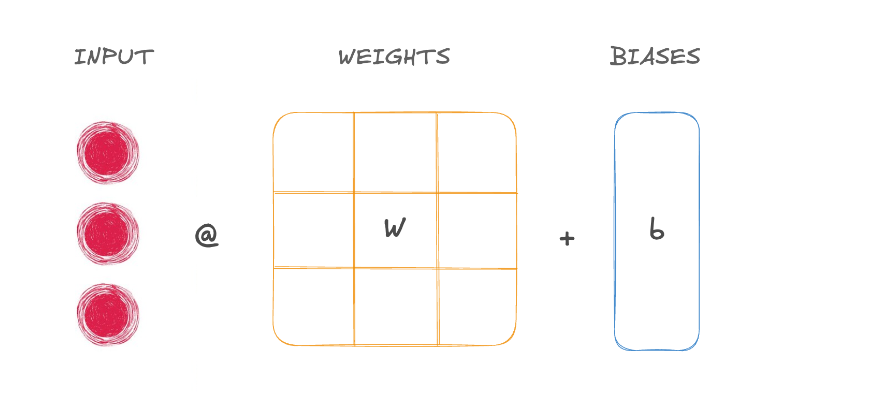
Networks with only linear layers are called fully connected.
Linear layers have connections (or arrows) between each input and output neuron, making them fully connected.

To stack multiple layers use nn.Sequential()
model = nn.Sequential(
nn.Linear(10, 18),
nn.Linear(18, 20),
nn.Linear(20, 5)
)
Input 10 -> output 18 -> output 20 -> output 5

Activation functions (non-linear)

Activation functions add non-linearity to the network

Sigmoid function (usualy used for binary classification)

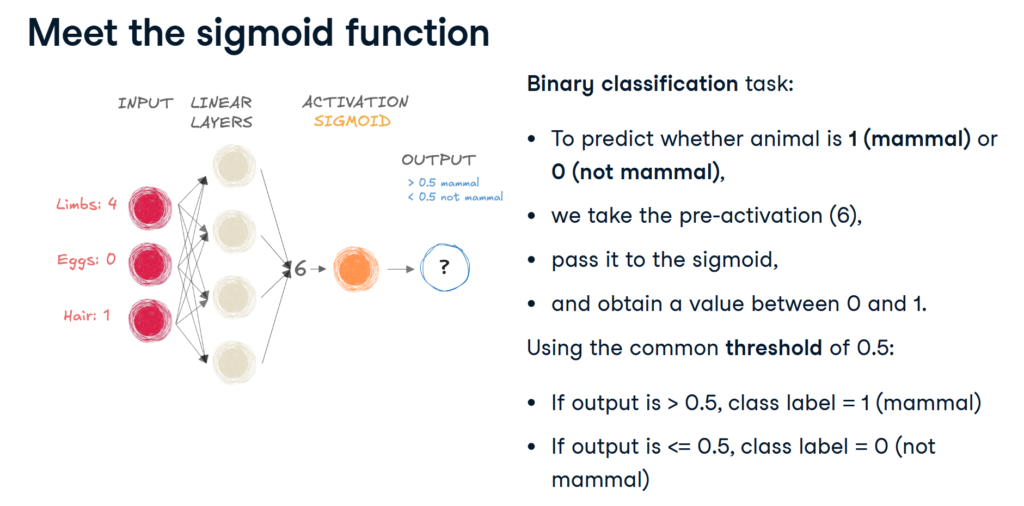
sigmoid = nn.Sigmoid()
nn.Linear(6,4)
nn.Linear(4,1)
output = sigmoid(input_tensor)

Softmax function (usualy used for multi-class classification)

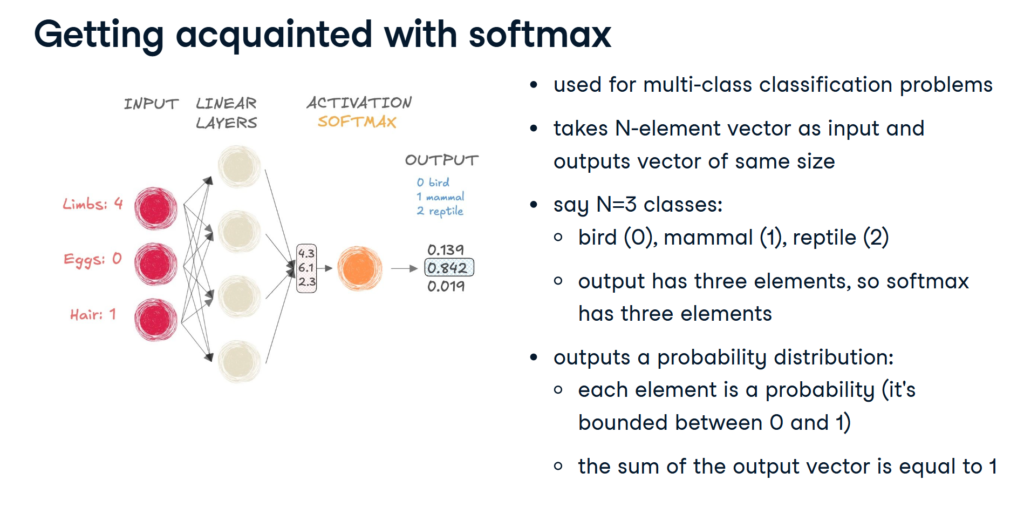
probabilities = nn.Softmax(dim=-1)
output_tensor = probabilities(input_tensor)

Celem uczenia ciągłego jest stopniowe powiększanie wiedzy modelu na podstawie nieskończonego źródła danych.

Zapominanie katastroficzne (catastrophic forgetting) jest zjawiskiem, w którym model ucząc się nowych lub kolejnych rzeczy, nadpisuje/zapomina nauczonych się wcześniej rzeczy.

Rozróżniamy trzy podstawowe „scenariusze” uczenia ciągłego:

Uczenie inkrementacyjne (task-incremental learning)

Model uczy się za pomocą różnych tasków rozpoznawania, estymacji, np klasyfikacja zwierzat w każdym tasku:

Task 1	Task 2	Task 3
Pies, Kot	Koń, Sarna	Królik, ptak

Celem uczenia sekwencyjnego jest rozszerzenie możliwości modelu wraz z zachowaniem obecnej wiedzy nauczonych w poprzednich taskach.

Jednym z efektywnych podejść jest jest zbudowanie indywidualnej sieci lub podsieci dla każdego z tasków, natomiast prowadzi to do niekontrolowanego zwiększenia wzrostu pamięci.

Metodami SOTA (State-of-the-art) są zbudowanie indywidualnych modeli dla każdego z tasków.

Obecnymi bottleneckami są:
Złożoność pamięciowa (…)

Uczenie domenowe (Domain-incremental learning)

Model uczy się na podstawie tasków tego samego rodzaju, ale w innym kontekście np. rozpoznawanie określonego obiektu na zewnątrz, a później w pomieszczeniu.

Uczenie klasowe (class-incremental learning)

Model uczy się ?

W przypadku, gdy model uczony jest na „obecnie aktualnych” danych, np. rozpoznawanie spamu, wykrywanie przestępstw finansowych, rozpoznawanie modeli samochodów może okazać się, że model ten będzie działać coraz gorzej z czasem, ponieważ struktura spamu, sposoby przestępstw czy wyglądy samochodów mogą drastycznie się zmienić przez co nasz model może przestać być użyteczny.

W skrócie jest to kwestia pogorszenia dokładności predykcji w czasie pod wpływem zmiany danych.

Istotne jest odpowiednie wczesne wykrywanie pogorszenia predykcji, ich powodu, zanim stanie się to poważnym problemem.

Concept Drift – Zmiana P(X|Y) zachowań, natomiast zmieniają się relacje, nie dane wejściowe. Zmiana kryteriów przyznania kredytów, np. przez podwyższenie stóp procentowych lub rekomendacji KNF, wymagane są teraz wyższe dochody lub z konkretnych źródeł np. UoP.


Data Drift możemy podzielić na:
Label Drift:
P(Y) zmienia się, czyli wynik naszego modelu. Np. zwiększenie się liczb zapytań kredytowych bez znaczących zmian makroekonomicznych.

Feature Drift:
P(X) zmienia się, czyli dane, na podstawie których wykonywana jest predykcja np. inny target klienta składa wnioski o pożyczkę. (np. BK2 – bardzo młodzi ludzie).

Virtual Drift:
Sytuacja, w której zmieniły się dane wejściowe, natomiast nie pogorszyło to predykcji, natomiast powinniśmy być w stanie to wykryć, aby móc odpowiednio wcześnie zareagować.